Pengertian Matriks

Dalam kehidupan sehari-hari kita sering menjumpai informasi yang disajikan dalam bentuk tabel.
Banyak informasi yang sering disajikan dalam bentuk tabel, diantaranya data rekening telepon, data tagihan listrik, data tabungan, harga penjualan barang, data absensi siswa dan lain-lain. Sebagai ilustrasi awal untuk memahami pengertian matriks, pelajari uraian berikut.
Diketahui data hasil panen seorang petani, selama tiga bulan berturut-turut, disajikan dalam tabel berikut (dalam ton).

Hasil Panen	Bulan pertama	bulan kedua	bulan ketiga
jeruk	10	8	12
mangga	5	14	9

Berdasarkan Tabel diatas, kita pasti memperhatikan setiap keterangan yang ada terkait banyaknya setiap buah yang dipanen dalam bentuk angka yang tertera pada tabel yang disusun letaknya berdasarkan baris dan kolom.
Tabel yang baru kita baca dapat disederhanakan dengan menghilangkan keterangan-keterangan yang terdapat pada tabel, dan mengganti tabel dengan tanda kurung seperti berikut ini.


Kini, data yang telah diubah bentuknya hanya terdiri atas bilangan-bilangan yang disusun menurut baris dan kolom. Bentuk baru seperti inilah yang dinamakan sebagai matriks.
Sebuah matriks memuat tanda kurung sebagai pembatas. Tanda kurung yang digunakan dapat berupa tanda kurung biasa ataupun tanda kurung siku.

Berikut ini beberapa pengertian tentang matriks :

• Matriks adalah himpunan skalar (bilangan riil atau kompleks) yang disusun atau dijajarkan secara empat persegi panjang menurut baris-baris dan kolom-kolom.
• Matriks adalah jajaran elemen (berupa bilangan) berbentuk empat persegi panjang.
• Matriks adalah suatu himpunan kuantitas-kuantitas (yang disebut elemen), disusun dalam bentuk persegi panjang yang memuat baris-baris dan kolom-kolom.
• Sekumpulan bilangan yang disusun berdasarkan baris-baris dan kolom-kolom membentuk pola persegi panjang dan ditulis dalam tanda kurung biasa maupun kurung siku.

Notasi yang digunakan






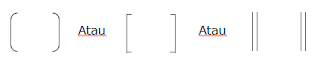
Telusuri
Pengertian Matriks, Jenis-jenis matriks, macam-macam matriks, notasi matriks, kesamaan dua matriks, operasi pada matriks, opersi matriks, matriks identitas, matriks segitiga, penjumlahan matriks, pengurangan matriks, penjumlahan dan pengurangan matriks, perkalian matriks, invers matriks, transpose matriks,