Trigonometri (Pembahasan SP 1 kelas 11 IPA)

No.1
sin 15° = p
dengan bantuan segitiga siku-siku, maka

Dari gambar diatas diperoleh

cos 15°

=

Sehingga:

Sin 75°	=	sin (90 – 15)°
	=	cos 15°
	=

No.2

Sin 65°. Cos 50° + cos 65°. Sin 50°	=	sin (65° + 50°)
	=	sin (90° + 25°)
	=	cos 25°

No.3

cos4 15° - sin4 15°	=	(cos2 15° - sin2 15°)(cos2 15°+ sin2 15°)
	=	cos 2(15°)
	=	cos 30°
	=

No.4



No.5

sin 2x = sin 30°
2x = 30°+n.360°
x = 15°+n.180°
untuk n=0 → x = 15°

2x =(180-30)°+ n.360°
2x = 150°+ n.360°
x = 75°+ n.180°
untuk n=0 → x = 75°
sehingga jumlah nilai x adalah 15° + 75° = 90°

No.6

Dengan membagi persamaan (1) dan (2) diperoleh

Dengan bantuan segitiga siku-siku, maka

dari segitiga siku-siku diatas didapatkan:

Kemudian, subtitusikan nilai sin 1/2(x-y) ke persamaan (1), sehingga:



No.7



No.8

karena  270°< 2A <360°  →  135° < A <180°  →   sin  bernilai (+) sehingga sin A = 1/3

No.9




No.10



left

Read more...

Contoh Soal (Menentukan Peluang)

Berikut ini pembahasan soal dari Lembar Kerja Siswa (LKS) kelas 11 IPA bab peluang. Semoga bermanfaat...

NO. 1
jika disediakan 9 angka, yaitu 1, 2, 3, ...., 9 akan dibentuk bilangan dengan 5 angka dan tidak boleh ada angka yang sama.
a. berapa banyak bilangan yang dapat dibentuk?
b. berapa banyak bilangan yang dapat dibentuk, jika bilangan itu habis dibagi 5
c. berapa banyak bilangan yang dapat dibentuk, jika bilangan itu tidak habis dibagi 5.
penyelesaian
a. banyak bilangan yang dapat dibentuk:
cara I

Sehingga banyak bilangan yang etrbentuk = 9. 8. 7. 6. 5 = 15120 cara

Cara II


b.banyak bilangan yang habis dibagi 5 yang dapat dibentuk:
bilangan yang habis dibagi dengan 5 adalah angka memiliki angka terakhir 5, sehingga

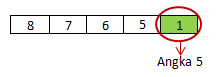
Sehingga banyak bilangan yang etrbentuk = 8. 7. 6. 5. 1 = 1680 cara

c.banyak bilangan yang tidak habis dibagi 5 yang dapat dibentuk:
= 15120 - 1680 = 13440


NO. 2
(Maaf, saya lupa soal lengkapnya. Kurang lebih seperti ini)
Jika sebuah mata uang dan sebuah dadu dilemparkan secara bersama-sama, tentukan peluang dari:
a. Muncul gambar pada mata uang dan angka ganjil pada dadu
b. Muncul Angka pada mata uang dan angka kurang dari 6 pada dadu
penyelesaian
a. Muncul gambar pada mata uang dan angka ganjil pada dadu

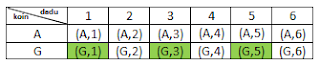
A = Kejadian muncul gambar pada mata uang dan angka ganjil pada dadu
A = {(G,1), (G,3), (G,5)}


b. Muncul Angka pada mata uang dan angka kurang dari 6 pada dadu

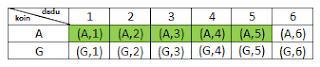
B = Kejadian muncul Angka pada mata uang dan angka kurang dari 6 pada dadu
B = {(A,1), (A,2), (A,3), (A,4), (A,5)}



NO. 3
Dalam sebuah kotak terdapat 6 bola merah dan 4 bola biru. Diambil dua buah bola satu demi satu tanpa pengembalian. Berapa peluang yang terambil itu
a. bola merah pada pengambilan pertama dan bola biru pada pengambilan ke dua
b. bola biru pada pengambilan pertama maupun ke dua

penyelesaian
a. peluang terambilnya bola merah pada pengambilan pertama dan bola biru pada pengambilan ke dua


b. peluang terambilnya bola biru pada pengambilan pertama maupun ke dua

Read more...

Notasi Matriks

Matriks kita beri nama dengan huruf besar seperti A, B, C, dll. Sedangkan elemennya dinotasikan dengan huruf kecil. Matriks yang mempunyai i baris dan j kolom ditulis A=(aij ), artinya suatu matriks A yang elemen-elemennya aij dimana indeks i menyatakan baris ke i dan indeks j menyatakan kolom ke j dari elemen tersebut.
Secara umum, matriks dengan m baris dan n kolom dapat disajikan sebagai berikut.



Matriks A=(aij ), i=1, 2, 3,…..m dan j=1, 2, 3,……., n yang berarti bahwa m adalah banyaknya baris dan n banyaknya kolom.

Ukuran matriks	2 x 2	2 x 1	2 x 3
Jumlah baris	2	2	2
Jumlah kolom	2	1	3

Matriks yang hanya mempunyai satu baris disebut MATRIKS BARIS, sedangkan matriks yang hanya mempunyai satu kolom disebut MATRIKS KOLOM. Dua buah matriks A dan B dikatakan SAMA jika ukurannya sama (mxn) dan berlaku aij = bij untuk setiap i dan j

Contoh Soal:
1. Diketahui matriks

Tentukan
a. ordo matriks M
b. banyaknya Elemen pada matriks M tersebut.
c. Nilai m₁₂ dan m₂₃

Jawab:
a. Karena matriks M mempunyai 2 baris dan 3 kolom, maka matriks M berordo 2x3
b. Matriks M mempunyai 6 elemen
c. m₁₂ artinya elemen yang berada pada baris ke-1 dan kolom ke-2 sehingga m₁₂=-1. m₂₃ artinya elemen yang berada pada baris ke-2 dan kolom ke-3 sehingga m₂₃=5.

2. Tentukan matriks koefisien dari sistem persamaan linear berikut.
2x + 3y – z = 6
4x – y + 3z = 10
–x + 2y – 3z = –9

Jawab:
Matriks koefisien dari sistem persamaan tersebut adalah








Telusuri
Pengertian Matriks, Jenis-jenis matriks, macam-macam matriks, notasi matriks, kesamaan dua matriks, operasi pada matriks, opersi matriks, matriks identitas, matriks segitiga, penjumlahan matriks, pengurangan matriks, penjumlahan dan pengurangan matriks, perkalian matriks, invers matriks, transpose matriks,

Read more...

Pengertian Matriks

Dalam kehidupan sehari-hari kita sering menjumpai informasi yang disajikan dalam bentuk tabel.
Banyak informasi yang sering disajikan dalam bentuk tabel, diantaranya data rekening telepon, data tagihan listrik, data tabungan, harga penjualan barang, data absensi siswa dan lain-lain. Sebagai ilustrasi awal untuk memahami pengertian matriks, pelajari uraian berikut.
Diketahui data hasil panen seorang petani, selama tiga bulan berturut-turut, disajikan dalam tabel berikut (dalam ton).

Hasil Panen	Bulan pertama	bulan kedua	bulan ketiga
jeruk	10	8	12
mangga	5	14	9

Berdasarkan Tabel diatas, kita pasti memperhatikan setiap keterangan yang ada terkait banyaknya setiap buah yang dipanen dalam bentuk angka yang tertera pada tabel yang disusun letaknya berdasarkan baris dan kolom.
Tabel yang baru kita baca dapat disederhanakan dengan menghilangkan keterangan-keterangan yang terdapat pada tabel, dan mengganti tabel dengan tanda kurung seperti berikut ini.


Kini, data yang telah diubah bentuknya hanya terdiri atas bilangan-bilangan yang disusun menurut baris dan kolom. Bentuk baru seperti inilah yang dinamakan sebagai matriks.
Sebuah matriks memuat tanda kurung sebagai pembatas. Tanda kurung yang digunakan dapat berupa tanda kurung biasa ataupun tanda kurung siku.

Berikut ini beberapa pengertian tentang matriks :

• Matriks adalah himpunan skalar (bilangan riil atau kompleks) yang disusun atau dijajarkan secara empat persegi panjang menurut baris-baris dan kolom-kolom.
• Matriks adalah jajaran elemen (berupa bilangan) berbentuk empat persegi panjang.
• Matriks adalah suatu himpunan kuantitas-kuantitas (yang disebut elemen), disusun dalam bentuk persegi panjang yang memuat baris-baris dan kolom-kolom.
• Sekumpulan bilangan yang disusun berdasarkan baris-baris dan kolom-kolom membentuk pola persegi panjang dan ditulis dalam tanda kurung biasa maupun kurung siku.

Notasi yang digunakan






Telusuri
Pengertian Matriks, Jenis-jenis matriks, macam-macam matriks, notasi matriks, kesamaan dua matriks, operasi pada matriks, opersi matriks, matriks identitas, matriks segitiga, penjumlahan matriks, pengurangan matriks, penjumlahan dan pengurangan matriks, perkalian matriks, invers matriks, transpose matriks,

Read more...

Integral taktentu dari sebuah fungsi

Integral sering disebut sebagai anti turunan. Integral taktentu dari sebuah fungsi dinotasikan dengan ʃ f(x)dx (baca: integral f(x) terhadap x). Notasi "ʃ...dx" diperkenalkan pertamakali oleh Leibniz yang digunakan untuk menyatakan integral.

Definisi: Himpunan Semua Fungsi yang turunannya sama dengan f(x) adalah integral dari f(x) dan dinotasikan dengan ʃ f(x)dx. Dengan kata lain: Jika F'(x)=f(x), maka ʃ f(x)dx =F(x)+C

Contoh:
1. Jika f(x)=4x → f'(x)=4, dengan demikian maka bisa dikatakan ʃ4dx=4x+C
2. Jika f(x)=3x² → f'(x)=6x, dengan demikian maka bisa dikatakan ʃ6x dx=3x²+C
3. Jika f(x)=6x²+2 → f'(x)=12x, dengan demikian maka bisa dikatakan ʃ12x dx=6x²+C


Rumus Dasar Integral taktentu
Berdasarkan penjelasan diatas, maka dapat diperoleh sebuah rumus dasar yang dapat digunakan untuk menentukan hasil dari integral. Rumus dasar Integral tersebut dinyatakan sebagai:

untuk n ≠ -1 dan c sebagai konstanta

Contoh 1:
Tentukan hasil dari ʃ6x²dx
Penyelesaian:


Contoh 2:
Tentukan hasil dari ʃ4x^-3dx
Penyelesaian:


Berikut ini beberapa teorema yang akan membantu dalam pengerjaan hitung integral.
Teorema 1
untuk n ≠ -1 dan c sebagai konstanta

Teorema 2

Jika f fungsi yang terintegralkan dan k suatu konstanta, maka ʃk. f(x)dx = k ʃf(x)dx

Teorema 3

Jika f dan g fungsi-fungsi yang terintegralkan, maka ʃ (f(x) + g(x))dx = ʃf(x)dx + ʃg(x)dx

Teorema 4

Jika f dan g fungsi-fungsi yang terintegralkan, maka ʃ (f(x) - g(x))dx = ʃ f(x)dx - ʃ g(x)dx

Teorema 5

Aturan integral parsial Jika u dan v fungsi-fungsi yang dapat didiferensialkan, maka ʃ u dv = uv - ʃv du

Teorema 6

Aturan integral trigonometri ʃ cos x dx = sin x + c ʃ sin x dx = - cos x + c

Read more...

Pertidaksamaan Kuadrat dan Cara Menyelesaikannya

Suatu kalimat terbuka yang memuat variabel dengan pangkat positif dan memiliki pangkat tertinggi dua dihubungkan dengan tanda disebut pertidaksamaan kuadrat.
Bentuk umum pertidaksamaan kuadrat :
ax² + bx + c > 0
ax² + bx + c ≥ 0
ax² + bx + c < 0
ax² + bx + c ≤ 0
dengan a, b, dan c∈ R dan a ≠ 0.

Cara Menyelesaikan Pertidaksamaan Kuadrat
Menyelesaikan pertidaksamaan kuadrat lebih mudah apabila menggunakan garis bilangan. Menentukan himpunan penyelesaian pertidaksamaan kuadrat berbeda dengan menentukan himpunan penyelesaian pertidaksamaan linear.
Pada pertidaksamaan linear, Anda dapat langsung menentukan daerah penyelesaian setelah memperoleh himpunan penyelesaiannya. Adapun pada pertidaksamaan kuadrat Anda harus menentukan daerahnya terlebih dahulu untuk dapat menentukan himpunan penyelesaiannya. Berikut ini beberapa langkah yang harus dipahami dalam menyelesaikan pertidaksamaan kuadrat.

1. Nyatakan bantuk pertidaksamaan kuadrat dengan cara menjadikan ruas kanan sama dengan nol 
2. Tentukan akar-akar dari pertidakasamaan kuadrat dengan cara memfaktorkan, melengkapkan kuadrat sempurna, atau rumus abc 
3. Tentukan nilai-nilai pembuat nol dari akar-akar petidaksamaan kuadrat pada tahap b. 
4. Gambarkanlah nilai-nilai pembuat nol yang diperoleh pada langkah 3 pada diagram garis bilangan 
5. Tentukanlah tanda di daerah sekitar pembuat nol, yaitu (+) dan (-) dengan cara menyubstitusikan nilai x yang lebih besar atau lebih kecil dari x₁ atau x₂. 
6. Himpunan penyelesaian dari suatu pertidaksamaan dilihat dari tanda pertidaksamaannya. Jika tandanya < atau ≤ maka daerah hasil yang dimaksud adalah daerah negatif. Dan jika tandanya > atau ≥ maka daerah hasil yang dimaksud adalah daerah negatif. Himpunan penyelesaian dari pertidaksamaan tersebut dinyatakan dalam bentuk interval.

Contoh:
1. Tentukan himpunan penyelesaian dari pertidaksamaan x² –5x –14 ≤ 0,
untuk x∈ R.
Jawab:
x² –5x –14 ≤ 0
x² –5x –14 ≤ 0
(x –7) (x + 2) ≤ 0
x₁ = 7 x₁ = –2

Uji daerah penyelesaian dengan cara mengambil sembarang titik selain 7 dan -2. Misalnya kita akan mengambil nilai x = 0.
x = 0 ⇒ x² – 5x –14 = 0² – 5.0 – 14 = –14 (negatif)

pada garis bilangan diatas angka 0 berada diantara -2 dan 7, sehingga daerah diatara -2 sampai 7 bernilai negatif (-)

Karena x² –5x –14 ≤ 0, maka daerah yang kita ambil adalah yang bernilai negatif (-)
Jadi himpunan penyelesaiannya adalah { x | –2 ≤ x ≤ 7, x∈ R}.


2. Tentukan himpunan penyelesaian dari pertidaksamaan
2x² + 5x + 15 < 3x² + 5x – 1, untuk x∈ R.
Jawab:
2x² + 5x + 15 < 3x2 + 5x –1
2x² + 5x + 15 –3x2 –5x + 1 < 0
–x² + 16 < 0
x² –16 > 0
(x – 4) (x + 4) > 0

x = 4 atau x = –4
Uji daerah penyelesaian dengan cara mengambil sembarang titik selain 7 dan -2. Misalnya kita akan mengambil nilai x = 0.
ambil x = 0 ⇒ x² –16 = 0² –16 = –16 (negatif)

Jadi, himpunan penyelesaian adalah {x | x < –4 atau x > 4, x ∈ R}.

3. Himpunan penyelesaian dari pertidaksamaan x² + 4x –12 ≤ 0, untuk x∈ R adalah ....
Jawab:
x² + 4x –12 ≤ 0
x² + 4x –12 ≤ 0
(x + 6) (x – 2) ≤ 0
x + 6 = 0 atau x – 2 = 0
x = – 6 atau x = 2
Uji daerah penyelesaian dengan cara mengambil sembarang titik selain 7 dan -2. Misalnya kita akan mengambil nilai x = 0.
ambil x = 0 ⇒ x² + 4x –12 = 0² + 4.0 –12 = –12 (negatif )

Jadi, himpunan penyelesaiannya adalah {x | –6 ≤ x ≤ 2, x∈ R}

Read more...

Himpunan Penyelesaian Pertidaksamaan

Himpunan penyelesaian dari pertidaksamaan dapat digambarkan pada garis bilangan, khususnya untuk himpunan penyelesaian berupa interval. Batas-batas interval digambarkan dengan menggunakan tanda bulatan penuh atau bulatan kosong. Tanda bulatan penuh menunjukkan bilangan tersebut termasuk ke dalam himpunan penyelesaian, dan tanda bulatan kosong menunjukkan bilangan tersebut tidak termasuk ke dalam himpunan penyelesaian.
Berikut ini beberapa bentuk dari interval yang sering dijumpai dalam pertidaksamaan.

Macam-macam Garis Bilangan Himpunan

Interval tertutup

{x | a ≤ x ≤ b, x∈R} = [a, b]


Interval setengah tertutup

{x | a ≤ x < b, x∈R} = [a, b)



{x | a < x ≤ b, x∈R} = (a, b]



Interval terbuka

{x | a < x < b, x∈R} = (a, b)



Interval setengah garis

{x | x ≥ a, x∈R} = [a, ∞)



{x | x > a, x∈R) = ( a, ∞)



{x | x ≤ a, x∈R) = (-∞, a]



{x | x < a, x∈ R) = (-∞, a)

contoh:
Tentukan himpunan penyelesaian dan garis bilangan dari 3x + 4 ≥ 2x - 5, untuk setiap x∈ R.
Penyelesaian:

a.	3x +4	≥ 2x –5
	3x – 2x + 4	≥ 2x –2x–5	(kedua ruas dikurangi 2x)
	x + 4	≥ –5
	x + 4 –4	≥ –5 –4	(kedua ruas dikurangi 4)
	x	≥ –9

Himpunan penyelesaian
{x | x ≥ –9 x∈ R}

Read more...